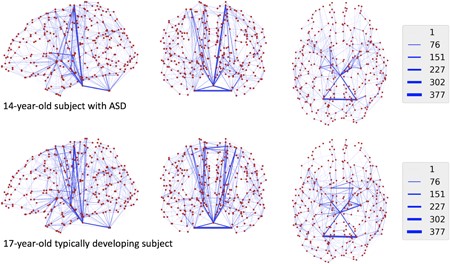
The field of neuroimaging dedicated to mapping connections in the brain is increasingly being recognized as key for understanding neurodevelopment and pathology. Networks of these connections are quantitatively represented using complex structures including matrices, functions, and graphs, which require specialized statistical techniques for estimation and inference about developmental and disorder-related changes. Unfortunately, classical statistical testing procedures are not well suited to high-dimensional testing problems. In the context of global or regional tests for differences in neuroimaging data, traditional analysis of variance (ANOVA) is not directly applicable without first summarizing the data into univariate or low-dimensional features, a process that may mask salient features of the high-dimensional distributions. In this work, we consider a general framework for two-sample testing of complex structures by studying generalized within- and between-group variances based on distances between complex and potentially high-dimensional observations. We derive an asymptotic approximation to the null distribution of the ANOVA test statistic, and conduct simulation studies with scalar and graph outcomes to study finite sample properties of the test. Finally, we apply our test to our motivating study of structural connectivity in autism spectrum disorder. Shinohara et al. (2019)